To follow up on the remarkable work Greg announced from Benedikt Bünz (Stanford)
and Jonathan Bootle (UCL) on Bulletproofs: https://eprint.iacr.org/2017/1066
Summary
=========
Over the last couple weeks, along with Jonas Nick, Pieter Wuille, Greg Maxwell
and Peter Dettmann, I've implemented the single-output version of Bulletproofs
at https://github.com/ElementsProject/secp256k1-zkp/pull/16 and have some
performance numbers.
All of these benchmarks were performed on one core of an Intel i7-6820MQ
throttled to 2.00Ghz, and reflect verification of a single 64-bit rangeproof.
Old Rangeproof 14.592 ms
with endo 10.304 ms
Bulletproof 4.208 ms
with endo 4.031 ms
ECDSA verify 0.117 ms
with endo 0.084 ms
Here "with endo" refers to use of the GLV endomorphism supported by the curve
secp256k1, which libsecp256k1 (and therefore Bitcoin) supports but does not
enable by default, out of an abundance of caution regarding potential patents.
As we can see, without the endomorphism this reflects a 3.47x speedup over
the verification speed of the old rangeproofs. Because Bulletproof verification
scales with O(N/log(N)) while the old rangeproof scales with O(N), we can
extrapolate forward to say that a 2-output aggregate would verify with 4.10x
the speed of the old rangeproofs.
By the way, even without aggregation, we can verify two rangeproofs nearly 15%
faster than verifying one twice (so a 3.95x speedup) because the nature of the
verification equation makes it amenable to batch verification. This number
improves with the more proofs that you're verifying simultaneously (assuming
you have enough RAM), such that for example you can batch-verify 10000
bulletproofs 9.9 times as fast as you could verify 10000 of the old proofs.
While this is a remarkable speedup which greatly improves the feasibility of
CT for Bitcoin (though still not to the point where I'd expect a serious
proposal to get anywhere, IMHO), the concerns highlighted by Greg regarding
unconditional versus computational soundness remain. I won't expand on that
more than it has already been discussed in this thread, I just want to tamp
down any irrational exhuberance about these result.
People who only care about numbers can stop reading here. What follows is a
discussion about how this speedup is possible and why we weren't initially
sure that we'd get any speedup at all.
Details
=========
Section 6 of the linked preprint discusses performance vs our old rangeproofs. As
Greg mentioned, it is possible to fit two 64-bit bulletproofs into 738 bytes,
with logarithmic scaling. (So one proof would take 674 bytes, but eight proofs
only 866 bytes.)
However, this section does not give performance numbers, because at the time
the preprint was written, there was no optimized implementation on which to
benchmark. It was known that verification time would be roughly linear in the
size of the proof: 141 scalar-multiplies for a 64-bit proof, 270 for an
aggregate of two proofs, and so on [*]. Our old rangeproofs required only 128
multiplies for a 64-bit proof, then 256 for two, and so on. So naively we were
concerned that the new Bulletproofs, despite being fantastically smaller than
the original rangeproofs, might wind up taking a bit longer to verify.
For reference, an ordinary ECDSA signature verification involves 2 multiplies.
So roughly speaking, the naive expectation was that a N-bit rangeproof would
require N-many signature verifications' worth of CPU time, even with this new
research. Worse, we initially expected bulletproofs to require 1.5x this much,
which we avoided with a trick that I'll describe at the end of this mail.
As you can see in the above numbers, the old rangeproofs actually perform worse
than this expectation, while the new Bulletproofs perform significantly **better**.
These are for the same reason: when performing a series of scalar multiplications
of the form
a*G + b*H + c*I + ...
where G, H, I are curvepoints and a, b, c are scalars, it is possible to compute
this sum much more quickly than simply computing a*G, b*H, c*I separately and
then adding the results. Signature validation takes advantage of this speedup,
using a technique called Strauss' algorithm, to compute the sum of two multiplies
much faster than twice the multiple-speed. Similarly, as we have learned, the
141 scalar-multiplies in a single-output Bulletproof can also be done in a single
sum. To contrast, the old rangeproofs required we do each multiplication separately,
as the result of one would be hashed to determine the multiplier for the next.
libsecp256k1 has supported Strauss' algorithm for two points since its inception
in 2013, since this was needed for ECDSA verification. Extending it to many points
was a nontrivial task which Pieter, Greg and Jonas Nick took on this year as part
of our aggregate signatures project. Of the algorithms that we tested, we found
that Strauss was fastest up to about 100 points, at which point Pippenger's was
fastest. You can see our initial benchmarks here
Loading Image...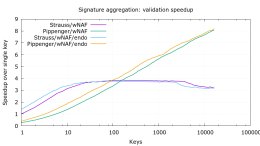
though this does not reflect some optimizations from Peter Dettmann in the last
week.
It was a happy coincidence that the Bulletproofs paper was published at nearly
the same time that we had working multi-point code to test with.
Finally, the Bulletproof verification process, as written in the paper, is a
recursive process which does not appear to be expressible as a single multiproduct,
and in fact it appears to require nearly twice as many multiplications as I claim
above. I want to draw attention to two optimizations in particular which made this
possible.
1. By expanding out the recursive process, one can see that the inner-product argument
(Protocol 1 in the paper) is actually one multiproduct: you hash each (L_i, R_i)
pair to obtain logarithmically many scalars, invert these, and then each scalar in
the final multiproduct is a product containing either the inverse or original of
each scalar.
Peter Dettmann found a way to reduce this to one scalar inversion, from which
every single scalar was obtainable from a single multiplication or squaring of a
previous result. I was able to implement this in a way that cached only log-many
previous results.
2. Next, line (62) of the Bulletproofs paper appears to require N multiplications
beyond the 2N multiplications already done in the recursive step. But since
these multiplications used the same basepoints that were used in the recursive
step, we could use the distributive property to combine them. This sounds
trivial but took a fair bit of care to ensure that all the right data was still
committed to at the right stage of proof verification.
Further Work
=========
There are still a few open issues I plan to help resolve in the coming month:
- Bulletproof aggregation is not compatible with Confidential Assets, where each
output has a unique asset tag associated with it. There are a couple possible
solutions to this but nothing public-ready.
- Bulletproofs, as described in the paper, work only when proving 2^n-many bits.
I believe there is a straightforward and verifier-efficient way to extend it
to support non-powers-of-2, but this requires some work to modify the proof in
the paper.
- Bulletproofs are actually much more general than rangeproofs. They can be used
to prove results of arbitrary arithmetic circuits, which is something we are
very interested in implementing.
[*] By "and so on", I mean that N bits require 2N + 2log_2(N) + 6 scalar multiplies.
Cheers
Andrew
--
Andrew Poelstra
Mathematics Department, Blockstream
Email: apoelstra at wpsoftware.net
Web: https://www.wpsoftware.net/andrew
"A goose alone, I suppose, can know the loneliness of geese
who can never find their peace,
whether north or south or west or east"
--Joanna Newsom